Elliptische Krommen : Een overzicht

Deze pagina was in eerste instantie bedoeld voor de docenten en andere belangstellenden die van plan waren om de tweedaagse cursus Is wiskunde nog wel mensenwerk? te volgen, georganiseerd door het C.W.I. (zie voor informatie vakantiecursus-2000.
Op 29 april 2001 heb ik enkele aanpassingen aangebracht. Diverse sites die niet meer bestonden heb ik verwijderd.
Hiermee geeft de site een goed overzicht over wat ik zal vertellen gedurende de kaleidoskoopdag van 3 mei 2001.
Op 11 april 2002 heb ik opnieuw enkele aanpassingen aangebracht. Bovendien is de tekst (ps) gz zip van de voordracht "Elliptic Curves, State of art" geplaatst.
Op 3 oktober 2002 heb ik wederom aanpassingen aangebracht en de tekst (ps) gz (200 kB) zip (200 kB) van de voordracht "Elliptic Curves and their application in cryptography" geplaatst.

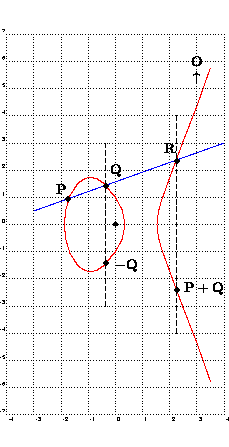
Op deze pagina treft u wat wetenswaardigheden aan t.a.v. elliptische krommen. We gaan op deze pagina niet in details treden. Zie daarvoor de tekst van de lezing en/of boeken en verwijzingen.

Records

Soort record	beschrijving	jaar
Punten tellen over F(2^n)	2^32003 door Argotech (Robert Harley). Argotech probeert Elliptische krommen in grote getale te verkopen aan bedrijven.	2001
Punten tellen over F(p)	10^499 door Reylard Lercier en François Morain.	1995
Discrete logaritme over F(2^n)	2^109 door Robert Harley, Damien Doligez, Daniel de Rauglaudre en Xavier Leroy.	2000
Discrete logaritme over F(p)	97-bits door Adrian Escott, John Sager, Alex Selkirk, Dimitris Tsapakidis en Robert Harley.	1998

Factoriseren met Elliptische Krommen

Elliptische krommen kunnen ook worden toegepast om getallen te ontbinden in factoren. Deze manier van factoriseren is niet zo goed om bijvoorbeeld RSA-getallen mee te kunnen factoriseren, maar kan wel goed worden gebruikt om getallen waarvan de kleinste priem tussen de 20 en 30 cijfers bevat te factoriseren. Zie hiervoor ecm. Op het ogenblik heeft R. Brent het record in handen met een factorisatie, waarbij de kleinste priem 50 digits bevat, zie Brent's artikel (Postscript document).

Tabel van Lenstra/Verheul
Tijd	RSA	ECC
1.11*10³	417	105
5.47*10³	488	110
7.80*10⁴	622	117
1.11*10⁶	777	124
7.80*10⁷	1068	140
3.22*10⁹	1369	160
1.33*10¹¹	1717	180
1.59*10¹³	2236	205
1.59*10¹⁶	3137	240

RSA versus Elliptische Krommen

Hiernaast staan in een tabel naast elkaar

Tijd
Is uitgedrukt in jaren op een Pentium 450 Mh machine met voldoende geheugencapaciteit die nodig is om RSA/ECC te breken.
RSA
Het aantal bits van de RSA-modulus.
ECC
Het aantal bits van de ECC-modulus.

Certicom had een fraai grafiekje waarin de tijden van RSA en ECC worden vergeleken op haar site staan.

Tabellen met aantallen punten op elliptische krommen

Abnormale Elliptische krommen (77 k)
Trace2 Elliptische krommen (25 k)

Om te downloaden

Ik heb twee programma's geschreven (geschikt om uit te proberen op een PC met Windows95).

Het eerste programma toont hoe twee punten op een elliptische kromme bij elkaar kunnen worden opgeteld.
elliptic.zip is 107 Kb groot.
Het tweede programma laat zien hoe elliptische krommen kunnen worden toegepast binnen de cryptografie. U kiest eerst een geschikte priem en kromme, die Ans en Bas zullen gebruiken. Vervolgens kiezen Ans en Bas geheime en (bijbehorende) publieke sleutels. Tenslotte kunt u berichten verzenden.
elgamal.zip is 144 Kb groot.
Overzichten van elliptische krommen over eindige lichamen met de priem tussen 5 en 47. Per combinatie van A en B wordt het aantal punten getoond en
eccview.zip is 38 Kb groot.

Aan te raden boeken en artikelen (verkrijgbaar op internet)

Public Key Cryptosystems using elliptic curves Afstudeerwerk van Johan Borst (TUE)
- Johan Borst
- Vrij verkrijgbaar in postscript-formaat
- 1997
- Dit werkstuk is goed leesbaar.
A Course in Number Theory and Cryptography
- Neal Koblitz
- ISBN 3-540-94293-9
- 1994
- Dit boek gaat in op de getaltheorie die schuil gaat achter de cryptografie. Er is ook een hoofdstuk gewijd aan elliptische krommen.
Algebraic Aspects of Cryptography
- Neal Koblitz
- ISBN 3-540-63446-0
- 1998
- Dit boek gaat veel dieper in op de wiskunde, waarop cryptografie is gebaseerd.
Elliptic Curve Public Key Cryptosystems
- Alfred J. Menezes
- ISBN 0-7923-9368-6
- 1993
- Dit boek is werkelijk prachtig, een uitstekende combinatie van elliptische krommen en cryptografie, maar tevens uiterst kostbaar. De auteur raadt het af om het aan te schaffen.
Implementing Elliptic Curve Cryptography
- Michael Rosing
- ISBN 1-8847-7769-4
- 1998
- Dit boek beschrijft hoe programmatuur t.a.v. elliptische krommen kan worden geschreven.
Elliptic Curves and Their Applications to Cryptography: An Introduction
- Andreas Enge
- ISBN 0-7923-8589-6
- 1999
- Ook dit boek is weer prijzig.

Verwijzingen naar pagina's over elliptische krommen

Elliptic Curve Cryptography door Integrity Sciences, Inc.
Online wordt een zeer korte uiteenzetting gegeven over elliptische krommen en cryptografie.
Elliptic Curve Cryptography Area door Certicom
Certicom is de organisatie die louter werkt met gepatenteerde toepassingen van Elliptic Curve Cryptografie. Op de bovengenoemde site wordt een overzicht gegeven t.a.v. de benodigde wiskunde, en de toepassingen in de cryptografie. Certicom looft geldprijzen uit voor de persoon (of groep) die als eerste in staat is om bepaalde discrete logaritme problemen voor elliptische krommen op te lossen.
Elliptic Curves and Cryptology door geocities
Deze pagina omvat een uitgebreide lijst van auteurs op het gebied van elliptische krommen. Ook staan op deze pagina diverse boeken genoemd en verwijzingen naar andere pagina's over elliptische krommen.

Verwijzingen naar pagina's over cryptografie

Pythagoras links over cryptografie
Compleet overzicht van alle aspecten van de cryptografie, overzichtelijk gerangschikt.

Terug naar mijn homepage

Last update: may 4, 2004